Ueli Raz
1 Musikalische Stimmungen
1.1 Die pythagoreische Stimmung
1.2 Die reine Stimmung
1.3 Die temperierte Stimmung
1.4 Erster Zusatz: Zum Verständnis der Centberechnungen
1.5 Zweiter Zusatz: Aufzeichnung der natürlichen, harmonischen Obertonreihe
Vorwort
Aus klimatischen und finanziellen Gründen sind die wissenschaftliche Sicherstellung und die kritische Transponierung bzw. Übersetzung der Quellen der indischen Musikgeschichte in einem prekären Zustand. Ohne philologische Erfahrung in den indischen Sprachen wäre es deswegen frivol, eine distanzierte Geschichte dieser Musik verbindlich skizzieren zu wollen. Der diskursive Umgang mit ihr sieht sich bis in die nähere Zukunft hinein zu einer pragmatischen Sichtweise gedrängt. Wenn hierbei einige Rätsel gelöst werden, ohne dass der Zauber der Raga-Kunstmusik an Glanz einbüßen muss, ist zur Annäherung an den kritischen Umgang mit Musik in Traditionen außerhalb Euroamerikas Genüge geleistet. Diese Einführungen drehen sich um Rätselfragen, die sich konkret in den Spielversuchen mit der Sitar herauskristallisieren: solche der Stimmung der Saiten, der Stimmung der Intervalle – und solche der zuweilen windschiefen Stimmung der in Europa Musizierenden, wie sie der holprige Zugang zu den Informationen und Materialien hervorruft.
Die Sanskrit- und Hindi-Ausdrücke sind englisch phonetisiert; in leicht fehlerhafter Weise wurde der nicht gesprochene Endungsbuchstabe „a“ in den Begriffen Raga und Tala als Ausnahmen beibehalten.
Bern, Oktober 1995
1 Musikalische Stimmungen
Dass die Elemente der Musik definiert werden, ist keine Selbstverständlichkeit, sondern eine Entdeckung bzw. Erfindung wie diejenigen des Feuers und des Rades. Kalte Gesellschaften (Lévi-Strauss), die durch Potlatch-ähnliche Ökonomien soziale Gefälle zu vermeiden trachten, kennen sie vielleicht überhaupt nicht, weil ein solches Wissen an eine musikalische Instrumentalpraxis gebunden ist, die nur an Institutionen der gesellschaftlichen Vermögensverwaltung mit einer akkumulativen Stoßrichtung hat kultiviert werden können. Umgekehrt sind in den Feudalgesellschaften die Theorien über Musik alle gleich, also unabhängig spezifischer kultureller Ausprägungen. Was in dieser Einleitung bezüglich einer allgemeinen Musikethnologie bzw. gemäß neuer Sprachregelung Ethnomusikologie dargestellt wird, ist ein physikalisches Wissen, das sowohl in der griechischen Antike wie in Indien und China in gleicher Weise diskutiert wurde. Die grundlegende Beobachtung betrifft den Zusammenhang zwischen den Schritten von einem Ton zu anderen Tönen – den Intervallen – und allgemeinen, d. h. mathematischen Proportionen.
Bei einem Monochord, das man sich gedanklich gut selbst vorstellen kann, wird eine Saite über zwei kantige Erhöhungen gespannt, die hier der Einfachheit wegen im Abstand von einem Meter positioniert sind; wird die Saite angezupft, ergibt das einen gewissen Ton, den man nun, damit die geläufige Musiksprache eingesetzt werden kann, mittels Saitenspannung bei einem C einstimmt. Wird die Saite genau in der Mitte niedergedrückt, entweder mit einem Finger bis zum Boden oder wie beim bottle-neck-Spiel der Gitarre mit einem harten Gegenstand (Flaschenhals, Schraubenzieher o. ä.), erklingt sie höher, im Vergleich mit anderen Tönen aber, die man auf dieselbe Weise produziert, qualitativ fast genau so wie die leere Saite. Die Feststellung des allgemeinen Zusammenhangs der Intervalle mit Proportionen und die der Besonderheit einiger Intervalle gegenüber anderen gehören aufs engste zueinander. Der neue Ton wird wiederum c genannt, jetzt klein geschrieben (das ist eine Konvention in der Notation, keine Erkenntnis). Er bildet die Oktave zum ersten, und mathematisch wird dieses Intervall mit
1:2 (oder 1/2)
wiedergegeben: wenn der neue Ton auf der Saite in einer gewissen Länge gemessen wird, so hat der Ausgangston die doppelte, hier also zwei mal 50 cm.
Ein anderes, qualitativ ebenso herausragendes Intervall, das auch von eher unmusikalischen Menschen leicht gesungen werden kann, ist die Quinte; sie liegt zwischen den beiden Oktavtönen, aber keineswegs exakt in der Mitte. [1] Wird die Proportion gemessen, findet man die Verhältniszahl
2:3;
die erklingende Saite ist 66, cm lang und heißt gemäß der Konvention G.
Etwas tiefer als die Quinte ist die Quarte positioniert, der Ton F. Die gemessene Saite ist 75 cm lang, im Verhältnis zur leeren Saite von einem Meter also 3:4.
Zugleich ist diese Quart auf verdeckte Weise wiederum eine Quint, diesmal nicht von der leeren Saite aus gemessen, sondern abwärts von der Oktave her. [2]
1. 1 Die pythagoreische Stimmung
Pythagoras (5. Jh. v. Chr.) hat ausschließlich mit jenen drei Intervallen alle 7 diatonischen, dann auch alle 12 chromatischen Töne der Oktave gemessen bzw. berechnet. [3] Man stelle sich ein Harfe vor, etwas höher als 1 Meter gebaut. Die fünftgrößte Saite wird auf einen Meter Länge gespannt, sie heiße wiederum C. Wo sich die Harfe verjüngt, wird eine 50 cm lange Saite gespannt, die Oktave c. Ungefähr in der Mitte zwischen den beiden ersten, etwas weiter Richtung Verjüngung, wird die G-Saite gespannt, die Quinte, 66, cm lang. In der Praxis ist dieses spitzfindige Längenmaß zwar nicht sinnvoll, weil die Spannung der Saite im Verhältnis zu ihrem Material und ihrer Dicke entscheidender ist als die Länge – doch lässt es sich trotzdem modellhaft an ihm orientieren, weil die Längenverhältnisse im Extremfall von günstigen Saiten nicht gänzlich zufällig sind und es eben die Demonstration nur allzu stark erleichtert, indem Hör- und Sichterfahrungen identisch bleiben (beim Monochord ist das Längenmaß ausschlaggebend, weil die eine Saite immer gleich stark gespannt ist). Wichtig ist, dass das Ohr die Quinte absolut eindeutig bestimmen kann. Dieselbe Positionierung geschieht mit dem Ton F. Jetzt sind vier Saiten gespannt, und dreizehn braucht es für alle chromatischen Töne der Oktave. Es wird nun von G aus die nächsthöhere Quint-Saite gespannt, also d, die dann mit einer neuen Saite eine Oktave tiefer neben die 1 Meter lange C-Saite aufgezogen wird; das ist jetzt die D-Saite, momentan die zweittiefste. Von hier aus wird wiederum eine Quint-Saite gespannt, das ist A. Noch einmal eine Quint höher ergibt e, eine Oktave erniedrigt E; von hier aus wird die Saite H gestimmt, dann fis mit anschließender Oktaverniedrigung, Fis. Die Harfe ist halbfertig, folgende Saiten sind montiert:
. . . . C . D . E F Fis G . A . H c . d . e . fis
Dieselbe Quintstimmung erfolgt nun abwärts vom Ton F aus, der ursprünglichen Quarte bzw. Abwärtsquint von c. Von F nach B1 und von hier eine Oktave erhöhen: B. Weiter von B nach Es, dann nach As1, eine Oktave erhöht: As, schließlich Des. Dadurch ist eine ganze Oktave mit den zwölf chromatischen Intervallen auf pythagoreische Weise gestimmt (die weiteren Saiten, die noch aufgezogen wurden, waren behelfsmäßig zur präzisen Abstimmung nötig).
Diese pythagoreische Stimmung ist sehr schön, und sie ist auch bis heute im Gebrauch, weltweit und in Europa. [4] Aber es sind zwei Töne komplett falsch, beim gewählten Vorgehen Des und As; ihr Intervall hat den Namen Wolfsquinte erhalten, weil es zum Heulen falsch klingt.
Dieser Fehler lässt sich sowohl verstehen wie mathematisch genau formulieren. Um die zwölf Töne der Oktave zu erhalten, wurden fortlaufend Quinten gebildet, außer der Transponierung um eine Oktave wurde diesem Verfahren nichts Weiteres hinzugefügt. Nach Vollzug eines solchen Vorgehens erklingt wieder der Anfangston; durch Unterlassung der Oktavtransponierung ist dieser Ton jetzt 7 Oktaven höher:
C G d a e1 h1 fis1 cis2 gis2 dis3 b3 f4 c5.
Die Töne C und c5 müssten identisch sein, sind es aber nicht. Die Abweichung lautet mathematisch:
Dies ist das pythagoreische Komma. Im modernen, unten erläuterten Maß beträgt es 23,46 Cent. Es lässt sich jetzt schon sagen, dass bei der temperierten Stimmung die Quinten nicht rein gestimmt werden, sondern
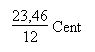
tiefer; auf diese Weise werden der Ausgangston C und die zwölfte Quint c5 qualitativ wieder identisch.
Jener „Fehler“, die „Irrationalität“ in der pythagoreischen Intervallbestimmung wurde schon zu Lebzeiten von den Schülern des Pythagoras diskutiert. Seit jener alten Zeit ist die Musiktheorie geprägt entweder durch eine empiristische oder dann eine mathematizistisch-rational-berechnende Distanzierung von Pythagoras, wobei nicht ohne weiteres erstens diese Tendenzen voneinander unterscheidbar sind und zweitens, damit zusammenhängend, es nicht eigentlich klar ist, was genau der Empirismus in der antiken und mittelalterlichen Akustik gewesen war – einer der Augen und/oder einer der Ohren – werden doch die physikalischen Apparaturen zur Messung der Frequenzen und der genauen Hörbarmachung der Obertöne erst im 19. Jahrhundert konstruiert.
Alle Intervallbestimmungen, die nicht-pythagoreisch und nicht-temperiert sind, heißen rein, mathematisch-rein oder natürlich-harmonisch. Wie die pythagoreischen sind auch diese in allen sog. Hochkulturen anzutreffen; besonders wild abgehandelt und nicht selten auch ins Absurde getrieben wurden sie im europäischen Mittelalter, in der Scholastik.
Entscheidend ist bei allen diesen Berechnungen bzw. Stimmanweisungen (für Orgeln und Klavichorde) der Miteinbezug der Terzen. Hat man auf dem Monochord mit der 1 Meter langen Saite die Intervalle der Oktave, der Quinte und der Quart bestimmt, als 1:2, 2:3 und 3:4, also 50 cm, 66, cm und 75 cm, dann findet man auch das ebenso angenehme und leicht zu singende Intervall der großen Terz erstaunlicher Weise in einem ganzzahligen Bruch, als 4:5.
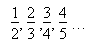
…das könnte langsam zu denken geben. Und in der Tat ist dies die Reihenfolge der Obertöne, die nichts anderes sind als die unendliche Vervielfachung der Grundfrequenz (in Hz): 1f, 2f, 3f, 4f, 5f, 6f etc.; die Intervalle zwischen den Obertönen als
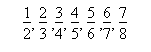
bilden dann diejenigen Verhältnisse, deren arithmetische Abweichungen voneinander regelmäßig kleiner werden als 1:1, 1:2, 1:3, 1:4, 1:5, 1:6, 1:7 etc.
Die Obertonreihe erscheint somit beinahe ähnlich einer Grenzwertkurve, bei der die einzelnen Schritte immer kleiner werden: 6:7 bis 11:12 sind Ganztonschritte, dann folgen Halbtöne, die immer weiter ins Mikroskopische abdriften – selbstverständlich sind diese Obertöne, mathematisch beschreibbar, empirisch nur mit modernen Apparaturen hörbar zu machen.
Man sieht jetzt die Ähnlichkeit der Ton- mit der Raumdistanz: ein ganzzahliges Vielfaches einer Frequenz führt diese zu einem nicht recht wahrnehmbaren Grenzwert wie sich die Messdistanz, der Meter, in der räumlichen Weite verliert. Wissenschaftshistorisch ist gänzlich der Problemhorizont der Neuzeit maßgebend: Leibniz und Newton.
Neben der Terz bleibt als Intervall noch die Sekunde; diese hat schon Pythagoras als das Intervall zwischen der Quarte und der Quinte bestimmt,
![]()
das Resultat ist im übrigen identisch mit der oben angewandten Rechnung 2/3 +2/3 –1/2 (Quinte mit Oktavtransponierung), also
2/3 x 2/3 x 2/1 = 8/9.
Die natürlich-harmonische Stimmung lautet nun C D E F G . . c als Abfolge der Intervalle bezüglich des Grundtons:
![]()
Werden diese Intervalle voneinander abgezogen, ergeben sich folgende Ganz- und Halbtöne:
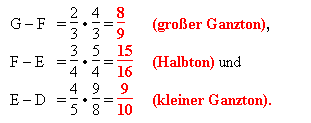
Auch diese reine Tonreihe hat also, sichtbar in der begrifflichen Unterscheidung ihrer Ganztöne, einen Fehler: ein Komma. Es ist der Abstand zwischen dem großen und dem kleinen Ganzton, D—E
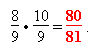
Dieses syntonische oder diatonische Komma beträgt 21,506 Cent.
Es ist vor allem diese Entdeckung, die in außereuropäischen Tonsystemen Antrieb zur Besonderung war, wie im indischen zur Definierung der Shrutis. Doch sind in diesen Systemen die Äquidistanzen nur ideell, nicht reell. Denn wenn die Oktave, um beim indischen Tonsystem zu bleiben, aus 22 Shrutis besteht, dann ergeben
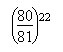
keineswegs eine Oktave, aber der konstatierbare Unterschied erlaubte offenbar bereits doch die konzeptuell verbindliche Postulierung von 4 Shrutis für den großen Ganzton, 3 für den kleinen, 2 für den Halbton. (Die Äquivokation im Begriff Shruti sei hier vorweggenommen: a) kleinste hörbare Tondifferenz, b) kleinste Maßeinheit des Tonsystems, c) Einheit des Tonsystems selbst, also jedwelcher Ton.)
Bei der hier erfolgten Konstruktion der natürlich-harmonischen Reihe fehlen noch die Töne des oberen Tetrachords A und H mit den Intervallen eines großen Ganztons, eines kleinen und eines Halbtones. Soll die Sext möglichst rein klingen, wird zwischen G und A der kleine Ganzton platziert, 9/10 dann der große für H mit dem nachfolgenden Halbtonschritt, 15/16.
Bezüglich des Grundtons bildet die Sext den Bruch
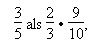
die Septime

Die Folge der Unterschiedlichkeit der Ganztöne bewirkt, dass die Quinte D—A äußerst dissonant klingt:
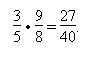
Da wie oben angetönt es nicht möglich ist, aus ganzzahligen Brüchen die Wurzel zu ziehen, gibt es keine reinen Halbtöne, deren Summe ein Ganzton wäre:
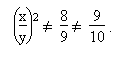
Umgekehrt liefert die Natur in den Obertönen eine Fülle von Mikrointervallen, deren Schatz in der Computermusik nur endlich gehoben werden müsste.
1. 3 Die temperierte Stimmung
Bei der temperierten Stimmung sind zwei geschichtliche Entstehungsmotive zu unterscheiden:
(1) der Wunsch nach Transponierbarkeit der Melodien auf alle Höhen fürs Zusammenspiel unterschiedlicher Instrumente und Stimmlagen (immer noch aktuell in der indisch-pakistanischen Musik mit Orgelbegleitung, wo sich die Tasteninstrumente zwar mikrotonisch bzw. rein stimmen lassen, die einmal gewählten Shrutis während des Spiels aber nicht mehr alterierbar sind) sowie
(2) der Wunsch zur Modulation, d. h. der Entfaltung der Tonalität in der Kompositionsweise.
Wegen des ersten Motivs gibt es seit dem frühen Mittelalter unzählige Theorien der Skalierung, die zugleich als praktische Anleitung zum Tastenbau und der Stimmung von Orgeln und Klavichorden dienten. [5] Das kompositorische Bewusstsein der äquidistanten Intervalle ist aber nicht vor Bachs Wohltemperiertem Klavier anzusetzen; die Dialektik der musikalischen Werkgeschichte ist also weitgehend unabhängig von den Erkenntnissen und Bestrebungen der physikalischen Musiktheorie.
Die modernen Berechnungen sind nicht radikal neu. Folgende Formeln bzw. Größen sind im Gebrauch, deren Bezug zu den oben dargestellten Verfahren leicht einzusehen ist:
![Textfeld: (1) Frequenz (n) = Schwingungszahl/Sekunde [Hz]
(2) Periode (T = 1n ) = Schwingungsdauer [msec]
(3) absolute Cents = Logarithmus zur Basis 12002 der Frequenz [Cabs]](ErstesKapitel-Dateien/image014.gif)
Die relativen Cents teilen die Oktave in 1200 Crel ein, den nunmehr als temperiert definierten Halbton in 100 Cent.
Für die reinen Intervalle ergibt sich folgende Liste:
| Oktave |
2/1 |
1200 Cent |
| Quinte |
3/2 |
701,955 Cent |
| Quarte |
4/3 |
498,045 Cent |
| pythagoreische Terz 9/8 • 9/8 |
81/64 |
407,820 Cent |
| gr. Terz |
5/4 |
386,314 Cent |
| kl. Terz |
6/5 |
315,641 Cent |
| Ganzton |
9/8 |
203,910 Cent |
Von den Halbtönen seien nur der diatonische, quasi natürliche und der pythagoreische, d. i. das Limma ausformuliert:
a) diatonischer Halbton = Quarte minus Terz =
![]()
b) Limma = pythagoreischer Halbton = Quarte minus pythagoreische Terz = „Rest“ =
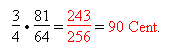
Mit Hilfe der Tabellen aus Reinecke (1970), um die man beim Studium der Mikrointervalle nicht herumkommt, sollten alle Berechnungen nachvollziehbar sein, die in antiken, scholastischen, neuzeitlichen und außereuropäischen Musiktheorien auftauchen oder bezüglich der Beschreibung von Obertonspektren in der Computermusik durchgeführt werden.
1. 4 Erster Zusatz: Zum Verständnis der Centberechnungen
Ausgangspunkt ist die Phänomenologie der reinen Intervalle:
Oktave = 2/1
Quinte = 3/2
Quarte = 4/3
¼
¼
¼
Werden die Intervalle als Strecken addiert, so werden rechnerisch die Brüche multipliziert. Geht man von einem Ton zu dessen Quarte und anschließend zu deren Quint, so wird die Oktave des Ausgangstons erreicht:
4/3 x 3/2 = 12/6 = 2
Innerhalb dieses Bereichs der Phänomenologie wird nach einem kleinsten Bruch gesucht, der die 12 gebräuchlichen Intervalle in all ihren Erscheinungen, d. h. sowohl rein wie pythagoreisch und temperiert, sinnvoll beschreibbar macht.
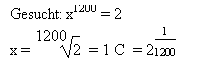
Da Cents Verhältniszahlen, Brüche sind, bilden ihre Summen Multiplikationen; mathematisch sind sie die Exponenten des kleinsten, bloß virtuellen Bruches, des einen Cents.
Definition:
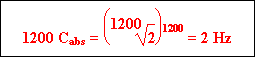
Bemerkung: Die Logarithmen entstanden aus den hohen Anforderungen der Handelsbuchrechnung in der Neuzeit; sie reduzieren die aufwendige Multiplikation auf Addition, die Division auf Subtraktion.
Da die herkömmlichen Logarithmentafeln auf der Basis von zehn berechnet sind, müssen solche mit der Basis
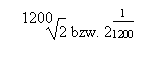
Die Formel heißt:
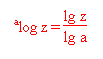
In absoluten Cent wird angegeben, wie oft das kleinste Intervall 21/1200 aneinandergefügt, d. h. mit sich selbst multipliziert werden muss, damit sich eine gesuchte Frequenz ergibt.
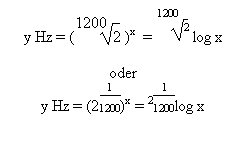
Während in diesem Funktionszusammenhang die x-Werte als Cents gleichmäßig weitergehen – und im temperierten System äquidistant, im gleichen Abstand die musikalischen Töne beschreiben – steigen die y-Werte als Hertz immer stärker an, und zwar in gleicher Weise, wo auch immer man einen Ausschnitt zur Illustration des Steigerungsgrades der Kurve wählt, eben
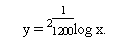

Wie wurde in diesem Beispiel der absolute Centwert für den Ausgangston 440 Hertz ausgerechnet?
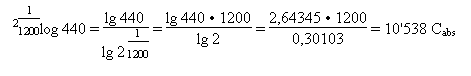
(Die Zehnerlogarithmen lg sind den gewöhnlichen Logarithmentafeln zu entnehmen.)
Der Rechnungszusammenhang mit den Bruchzahlen der reinen Intervalle bedingt das definitorische Frequenzmaß als Vermittelndes:
2 Hz = 1200 C
1 Hz = 0 C
Quinte = 3/2 = 1,5 Hz = x
Also:
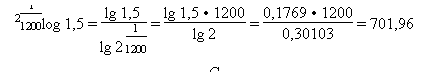
Quarte = 4/3 = 1 Hz = 498,045 C
…
…
…
Wiederholung:
1. Transkulturell wird die Oktave als Einheit erfahren, die selbst im Extremfall reiner Pentatonik durch zwölf benennbare Töne aufgeteilt ist. Die Töne können auch dann leicht benannt werden, wenn sie physikalisch differente Qualitäten aufweisen: eine Terz wird als Terz erkannt beziehungsweise zurechtgehört, handele es sich um eine pythagoreische, reine, temperierte oder „falsche“.
2. Wahrscheinlich in allen Kulturen gibt es das Metier der Musiktheorie, das mit den Attituden der Musikanten keineswegs zu korrespondieren braucht. Zu diesen Theorien gehört die Frage nach dem kleinsten hörbaren Intervall wie auch nach demjenigen, das als atomische Einheit konzipiert wird und mit welchem alle möglichen und musikalisch unmöglichen Intervalle beschrieben werden. Diesen Zweck erfüllt das Cent, 1200 für eine Oktave.
3. Die Zahl 12 ergibt sich aus der Einsicht in zwölf Tonnamen für eine Oktave, weltweit; die zwei Dezimalstellen sind pragmatisch begründet.
4. Wenn die Oktave aus 1200 gleichen Elementen besteht, wird ein einzelnes wie folgt verständlich: es ist dasjenige, welches zwei ergibt, wenn es 1200 Mal mit sich selbst multipliziert wird, oder eben
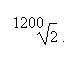
5. Wie die Addition mit der Subtraktion und die Division mit der Multiplikation verschwistert sind, ist das Rechnen mit Exponenten das Umgekehrte des Wurzelziehens: Wird die oben gesetzte Wurzel mit dem Exponenten 1200 versehen, ergibt sich 2:
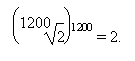
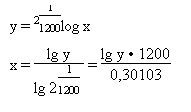
1. 5 Zweiter Zusatz: Aufzeichnung der natürlichen, harmonischen Obertonreihe
|
Oberton |
|
Tonhöhe |
|
Differenz in Cent = |
|
|
|
|
|
reine Intervalle |
|
1 |
440Hz = |
10'538Cabs = |
0Crel = |
|
|
2 |
880Hz = |
11'738Cabs = |
1200Crel = |
1200 |
|
3 |
1320Hz = |
12'440Cabs–11'738 = |
702Crel = |
702 |
|
4 |
1760Hz = |
12'938Cabs= |
1200Crel = |
498 |
|
5 |
2200Hz = |
13'324Cabs–12'938 = |
386Crel = |
386 |
|
6 |
2640Hz = |
13'640Cabs–12'938 = |
702Crel = |
316 |
|
7 |
3080Hz = |
13'906Cabs–12'938 = |
968Crel = |
266 |
|
8 |
3520Hz = |
14'138Cabs–12'938 = |
1200Crel = |
232 |
|
9 |
3960Hz = |
14'342Cabs–14'138 = |
204Crel = |
204 |
|
10 |
4400Hz = |
14'524Cabs–14'138 = |
386Crel = |
182 |
|
11 |
4840Hz = |
14'689Cabs–14'138 = |
551Crel = |
165 |
|
12 |
5280Hz = |
14'840Cabs–14'138 = |
702Crel = |
151 |
|
13 |
5720Hz = |
14'978Cabs–14'138 = |
840Crel = |
138 |
|
14 |
6160Hz = |
15'106Cabs–14'138 = |
968Crel = |
128 |
|
15 |
6600Hz = |
15'226Cabs–14'138 = |
1088Crel = |
120 |
|
16 |
7040Hz = |
15'338Cabs–14'138 = |
1200Crel = |
112 |
|
17 |
7480Hz = |
15'443Cabs–15'338 = |
105Crel = |
105 |
|
18 |
7920Hz = |
15'542Cabs–15'338 = |
204Crel = |
99 |
|
19 |
8360Hz = |
15'635Cabs–15'338 = |
297Crel = |
93 |
|
… |
|
|
|
|
|
… |
|
|
|
|
|
40 |
17'600Hz = |
16'924Cabs–16'538 = |
386Crel = |
|
|
41 |
18'040Hz = |
16'967Cabs–16'538 = |
429Crel = |
43 |
Die Werte sind nach den Tabellen in Reinecke (1970) bestimmt worden. Entscheidend ist die Kolonne mit den relativen Centangaben. Sie gibt eine Vorstellung davon, wie langsam nur die Intervalle kleiner werden.
Der Unterschied zwischen dem 40. und dem 41. Oberton ist nur knapp weniger als ein Viertelton (50 C). Das bedeutet, dass die Obertonreihe nicht im strengen Sinn als Grenzwertkurve zu verstehen ist, sondern einfach als geneigte, sich abflachende ohne anzeigbaren Grenzwert, der die Grundtöne zu spezifizieren vermöchte. Man muss wohl zugeben, dass die spekulativen, vom Ohr nicht wahrgenommenen sehr hohen Obertöne auch für die Musiktheorie nichts nutzen, weil sie eher dem physikalischen Rauschen zuzuordnen sind als einer noch zu realisierenden Musik.

Zur Funktion 3, den Obertönen in Abhängigkeit der Schwingungsperiode:
Die Proportionen der Obertöne beziehen sich weder auf die Frequenzen noch die Centwerte, sondern phänomenologisch auf die Länge einer Monochordsaite oder einer Luftsäule. Die Angabe der Periode, die diese „Längen“ ausdrückt, geschieht in Millisekunden. Der absolute Grenzwert ist immer gleich, nämlich Null. Also charakterisiert auch der Verlauf dieser „Grenzwertkurve“ die Obertonreihe eines musikalischen, d. h. reinen Tones nur auf sehr triviale Weise: von allen immer höher werdenden Tonreihen ist der Grenzwert Null.

[1] Das ist eine sehr wichtige Beobachtung: es gibt keinen Bruch, der mit sich selbst multipliziert 1/2 ergibt; es gibt auf diesem Feld der Beobachtung kein Intervall, das ein nächstgrößeres ergeben würde, wenn man es verdoppelte, genau gleich wie das räumliche Distanzbewusstsein nicht mit der Sicherheit eines Messintervalls aus der Nähe, also etwa einem Meter, die Anwendung eines anderen aus der Ferne, also etwa einem Kilometer, praktizieren kann.
[2] Man sieht hier, wie mit Proportionen, die nicht als Teile eines Ganzen gelten, zu rechnen ist: bei der Addition werden die Brüche multipliziert, bei der Subtraktion dividiert. Wenn die Oktave minus die Quinte eine Quarte ergibt, wird wie folgt gerechnet:
1/2 – 2/3 = 1/2 x 3/2 = 3/4
[3] Da die Quart eine umgekehrte Quint darstellt, benötigen die pythagoreischen Berechnungen streng genommen nur die Oktave und die Quint.
[4] Daniélou (1991a) bestimmt p. 48f alle indischen Shrutis durch reine Quinten, mit den rätselhaften fünf Aus-gangstönern
1/1, 2/5, 18/25, 5/6, 25/36
Für die indische Musik erscheint ein solch konsequenter Pythagoreismus allerdings wenig plausibel, da die Praxis, wie die vorliegenden Erläuterungen zeigen wollen, sich an einer diskreten Mischung von reinen und pythagoreischen Intervallen orientiert.
[5] Vgl. Lindley (1987). Hier ist auch eine Tabelle Newtons abgedruckt, die in weitsichtiger Vorwegnahme eine Art Centberechnung wiedergibt.